ماذا تعني فيزيائيا قوة كوريوليس وما مصدرها ؟

“كاسبار كوسطاف دو كوريوليس” : هو عالم رياضي فرنسي قد بين في القرن 19 أنه إذا كان جسم معين A يتحرك فوق سطح جسم آخر B في حالة دوران ، فإنه يجب الأخذ بعين الإعتبار تسارع ثانوي يعطي مسار منحني وهمي للجسم A و الذي ليس في الحقيقة الا مسار مستقيمي بالنسبة لمرجع غاليلي آخر وقد جعل هذا التسارع على شكل قوة وهمية سماها “قوة كوريوليس” .

ونأخذ كمثال على ذلك الأرض مثلا والتي هي جسم في حالة دوران حول نفسه ، الأرض في الحقيقة ليست مرجعا غاليليا ولكن على المدد الزمنية الصغيرة يمكن اعتبارها مرجعا غاليليا اما في حالة المدد الزمنية الكبيرة فهي ليست بمرجع غاليلي ولهذا فحركتها حول مركز دورانها لابد وأن تؤثر على اي شيء يسير في الجو المحيط بها و خاصة اذا كان يسير على مسافات طويلة و نخص بالذكر هنا المادة التي تكون الغلاف الجوي .

مثلا اذا كان شخص يوجد في احد قطبي الكرة الارضية ويريد أن يرمي كرة الى شخص اخر يوجد على خط الاستواء فالكرة لن تصل ابدا الى المكان الذي يوجد فيه الشخص لأن الوقت الذي تكون قد وصلت فيه الكرة سوف يكون الشخص تحرك من مكانه لأن الأرض تدور حول نفسها هنا نقصد المدد الزمنية الطويلة فقط اما في حالة ما اذا كانت الكرة سوف تصل في بضع دقائق فلن يكون هناك اي تأثير لقوة كوريوليس .

و لكي نكون أكثر دقة فالشخص الذي يوجد في احد اقطاب الارض فسرعته الافقية صفر لأنه يوجد على محور دوران الارض وكلما اتجهت نحو خط الاستواء كلما ازدادت السرعة الخطية الافقية لدوران الارض حتى تصبح في قيمتها القصوى عند خط الاستواء ثم تبدأ بالتناقص اذا استمريت في السير نحو القطب الآخر حتى تنعدم عند القطب الآخر لمحور الدوران . وهذا الفرق في السرعات الافقية لدوران الأرض على سطحها هو ما يجعل ان من يتجه عموديا على سرعة الدوران يتعرض لقوة كوريوليس .

عندما يصبح المرجع غير غاليلي تصبح حركة الاجسام فيه مستقلة عنه فإذا ما كان المرجع يقوم بحركة دوران فالأجسام التي تتواجد فيه لا ترغب في الدوران معه بل تريد ان تسير في مسار مستقيمي ولهذا فإذا كان جسم يوجد على سطح مرجع في حالة دوران سوف تلاحظ أن حركة الاجسام لا تسير في مسار مستقيمي في المرجع غير الغاليلي ولكن في الحقيقة اذا لاحظت حركتها بالنسبة الى مرجع غاليلي اخر سوف ترى ان حركة ذلك الجسم هي حركة مستقيمية. فهي تظهر غير مستقيمية فقط في المراجع غير الغاليلية ولكن تبقى حركتها في خط مستقيم بالنسبة الى المراجع الغاليلية !

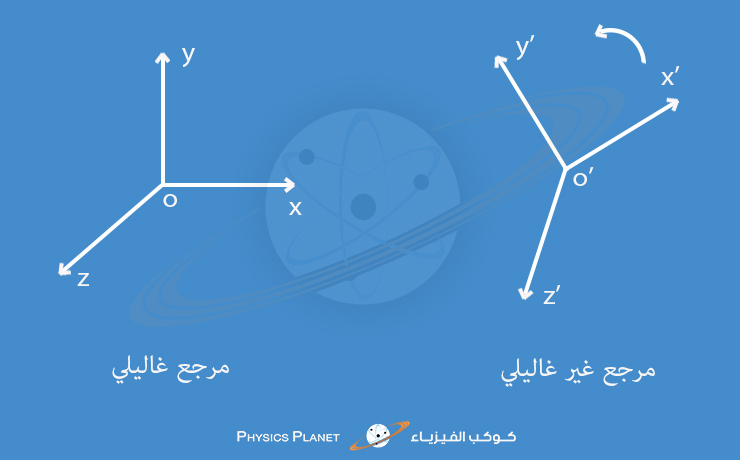
حركة الرياح في الجو تتم عن طريق اختلاف الضغط بين المناطق ، حيث ينتقل الهواء من المناطق ذات الضغط المرتفع نحو المناطق ذات الضغط المنخفض ، لكن على المسافات البعيدة جدا فإن هذه التيارات الهوائية تخضع لقوة كوريوليس لأن الأرض تصبح مرجع غير غاليلي مما نلاحظ و نحن على المرجع غير الغاليلي ان الرياح تقوم بالدوران عند الانتقال ولكن هي في الحقيقة بالنسبة لمرجع غاليلي خارجي تسير في مسار مستقيمي ولكن سطح الارض هو من يقوم بالدوران .

نعود الى صلب الموضوع مع تحليل المعادلات الرياضية للمزيد من التفاصيل حول ما تخفيه العلاقة التي تعطي طريقة حساب قيمة قوة كوريوليس.

أثناء دراسة نقطة مادية في الميكانيك التي يتم دراستها في الجامعة غالبا ما نصادم مراجع غاليلية وأخرى غير غاليلية .

نعتبر في حالتنا هذه أن هناك مرجع غاليلي ثابت وهناك مرجع اخر غير غاليلي يتحرك بالنسبة للمرجع الثابت ، المرجع غير الغاليلي يعتبر مرجع في تسارع بالنسبة للمرجع الغاليلي الثابت أي انه قد يكون يسير بسرعة غير منتظمة و يقوم بدوران اثناء تحركه كذلك .

اذا اعتبرنا نقطة مادية توجد في المرجع غير الغاليلي فإنها سوف تخضع للقوى القصورية الناتجة على تواجدها في مرجع غير غاليلي ومن هذه القوى الوهمية التي نقصدها هنا هوما القوتين الوهميتين :

قوة كوريوليس Fic و قوة اونترانمون Fie :
Fic = Force imaginaire de Coriolis
Fie = Force imaginaire d’entraînement

سوف نقتصر هنا على تفسير قوة كوريوليس ويمكنك بنفس الطريقة التحليلية ان نفسر القوة الاخرى .

يكتب تعبير قوة كوريوليس كالتالي :
Fic = -m.ɣc = -2m.ΩᴧVr
ɣc = 2.ΩᴧVr : تسارع كوريوليس

Ω : متجهة دوران المرجع غير الغاليلي بالنسبة للمرجع الغاليلي
Vr : سرعة الجسم بالنسبة للمرجع غير الغاليلي
m : كتلة الجسم المتواجد في المرجع غير الغاليلي

بالنسبة لتعبير القوة و التسارع و السرعات هنا فهما قيم متجهية اي توجد متجهة على كل من متجهة القوة Fic ومتجهة دوران المرجع Ω و السرعة النسبية للجسم Vr في المرجع غير الغاليلي .

كي نفسر معنى هذه القوة فيزيائيا يجب أن نقوم بتحليليها ونبين متى تكون منعدمة ومتى تكون غير منعدمة ؟

تنعدم هذه القوة في الحالات الثلاث التالية :

1- في حالة كانت السرعة النسبية للجسم Vr المتحرك في المرجع غير الغاليلي منعدمة .
2- في حالة كانت متجهة دوران المرجع غير الغاليلي Ω منعدمة (اي ان المرجع لا يقوم بالدوران حول اي محور من محاوره اثناء انتقاله ) .
3- في حالة كانت السرعة النسبية للجسم Vr متوازية مع متجهة الدوران (لأن الجداء المتجهي لمتجهتين متوازيتين منعدم ) .

اذن من خلال الحالات الثلاث يمكن أن نستنتج أن هذه القوة تنتج عن تسارع ثانوي ɣc ينتج عن تحرك الجسم في “مرجع غير الغاليلي في حالة دوران” .

لنفسر أكثر لكي ينتج تسارع كوريوليس على الجسم يجب أن يكون المرجع غير الغاليلي يقوم بالدوران اثناء انتقاله ، والجسم الذي يتواجد داخله في حالة حركة !

في حالة ما اذا كان المرجع غير الغاليلي لا يقوم بالدوران اثناء تسارعه (ازدياد في منظم السرعة فقط) فإن الجسم المتحرك داخله لن يشعر بقوة كوريوليس ، وفي حالة كان المرجع غير الغاليلي يقوم بالدوران ولكن الجسم لا يتحرك داخله فإنه لن يشعر بقوة كوريوليس كذلك.

اذا كان الجسم المدروس داخل المرجع غير الغاليلي الذي يقوم بالدوران حول نفسه هو ارنب مثلا فإذا ارادت الأرنب أن لا تشعر بقوة كوريوليس فيجب أن تبقى جالسة في مكانها ولا تتحرك داخله أو أن تتحرك داخله بشرط أن يكون المرجع لا يقوم بالدوران حول نفسه .
لكن لا يجب ان ننسى انها لن تشعر فقط بقوة كوريوليس اما قوة اونترانمون فهي موجودة حتى لو كان المرجع غير الغاليلي لا يقوم بالدوران .

الحالة الأخيرة هي حتى لو كان المرجع غير الغاليلي يقوم بالدوران اثناء انتقاله وكانت هذه الارنب تتحرك داخله بشرط ان تتحرك فوق محور الدوران او فوق محور اخر موازي له فلن تشعر في هذه الحالة بقوة كوريوليس . لأن السرعة و متجهة سرعة الدوران متوازيتان وجذاؤهما المتجهي منعدم .

تحرير : شعيب المستعين

ملاحظة: المتجهات نرمز لها بأحرف عريضة.