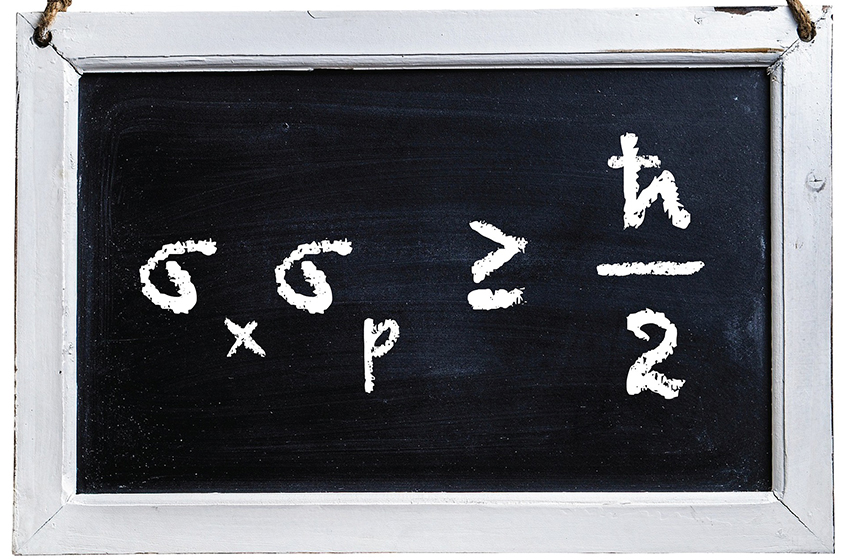مبدأ عدم التحديد لهايزنبرغ :
∆r.∆p ≥ ℏ/2
avec r = r(x,y,z) et p = p(x,y,z)
ℏ= h/2π et h = 6,62607015.10⁻³⁴ J.s
مبدأ عدم التحديد على المحور x :
∆x.∆pₓ ≥ ℏ/2
حيث أن :
∆pₓ=m.∆vₓ
أول ما كتب هايزنبرغ المبدأ المشهور تحت إسم “مبدأ الإرتياب” بالألمانية وشرح مفهومه، أستدرك بعد ذلك الخطأ الذي وقع فيه في اختيار الاسم، ثم بعد ذلك غير الاسم في الطبعة الثانية من الكتاب، لكن عندما تُرجمت طبعته الأولى إلى لغات أخرى كالفرنسية والانجليزية لم يتم تغيير الإسم في الطبعات المترجمة الأخرى واستمر نفس الإسم الأول ينتشر في باقي الترجمات، ولا أحد إنتبه أن هايزينبرغ أعاد تغيير الإسم في الطبعة الثانية في النسخة الالمانية من 《مبدأ الإرتياب》 إلى 《مبدأ عدم التحديد》.

• فما الذي جعله يتدارك هذا الخطأ ليعيد تغيير إسم المبدأ؟
لأنه أدرك بعد صدور النسخة الأولى أن الأغلبية فهموا هذا المبدأ بالطريقة الخطأ، إذ ظنوا أن ما ينص عليه هذا المبدأ هو أن هذا الارتياب ناتج عن قصور في أجهزة القياس فقط، بحيث أنها غير قادرة على تحديد سرعة الجسيم وموضعه في آن واحد. ولكن في الحقيقة لم يكن هذا هو المقصود في المبدأ، لأن ما يقول به المبدأ هو أن التكلم عن سرعة الجسم وموضعه في ميكانيك الكم لا معنى له، فقولنا بأنه كلما زادت معرفتنا حول موضع الجسيم تضاءلت معرفتنا حول سرعته يوحي وكأن للجسيم الكمي موضع! فقط أجهزتنا الرصدية ليست قادرة على تحديده بدقة، وهذا خطأ لأن المبدأ يقول لك بأن الجسيم الكمي ليس له موضع أصلا حتى نحاول تحديده، فهو جسيم غير مُمَوضع ولا يمكن أن نتكلم عن شيء إسمه موضع الجسيم في ميكانيك الكم.
فهذا المبدأ يتكلم عن عدم إمكانية التحديد وليس الارتياب في تحديد الموضع، وهذا ما دفع هايزنبرغ إلى إعادة تسمية المبدأ ب 《مبدأ عدم التحديد》، أي أن عدم التحديد في الموضع x∆ ضرب عدم التحديد في كمية الحركة pₓ∆ أكبر من أو يساوي ثابتة بلانك h.
∆x.∆pₓ ≥ ℏ/2
هذا المبدأ يُقرأ كالتالي : عدم التحديد في الموضع ضرب عدم التحديد في كمية الحركة أكبر من أو يساوي ثابت بلانك.
لاحظ جيداً أننا نتكلم هنا فقط عن عدم التحديد وليس عن ارتياب أو نسبية في تحديد الموضع! فالجسيم الكمي ليس له موضع أصلاً حتى نتكلم عن نسبية في تحديد موضعه، نحن نتكلم هنا عن عدم القدرة على التحديد في الموضع والذي نرمز له ب x∆ وعدم التحديد في كمية الحركة والتي نرمز لها بpₓ∆، لأن هذا الجسيم هو جسيم كمي غير يتميز بعدم التموضع، فلا يمكننا تشبيهه بالجسيم الكلاسيكي حيث نتكلم عن الموضع x وكمية الحركة p، وإلا فمفهوم الموجة بالنسبة للجسيم الكمي لن يبقى له معنى في ميكانيك الكم. الجسيمات الكمية جسيمات غير مُموضعة بطبيعتها وليس هناك أي موضع يمكن أن نقرنه بمكان تواجدها، فهي توجد على شكل موجات تحتل حجم معين تشغل فيه أماكن عدة في نفس اللحظة.
• مصطلحات
Principe d’incertitude : مبدأ الارتياب
Principe d’indétermination : مبدأ عدم التحديد
Localisé : مُمَوضع
Délocalisé : غير مُمَوضع
إعداد : شعيب المستعين
المراجعة اللغوية : نادية بوحفص