لا يمكنك أن تفكر كيف إستطاع شرودينغر الحصول على معادلته الشهيرة إن لم يسبق لك أن درست من قبل الموجات وخصائصهم بالمعادلات التفاضلية وحلول هذه المعادلات سواء الموجات الميكانيكية أو الكهرومغناطيسية، لأنه بالطريقة ذاتها تم إستنتاج معادلة شرودينغر وذلك حسب بعض المسلمات التي تم الانطلاق منها.

• البداية كانت مع المسلمة الشهيرة التي وضعها العالم الفرنسي لويس ديرولي : p = h/λ (1)

أو حسب الكتابة المفضلة في ميكانيك الكم : p =ℏk

مع أن : k = 2π/λ

و ℏ=h/2π

• المسلمة الثانية تتعلق بالطاقة الكلية للجسيمات والتي تم استنتاجها بناء على مسلمة لويس ديبرولي وهي التي أنتجت لنا معادلة شرودينغر : E =ℏω

كيف تم الحصول على هذه المسلمة ؟

حسناً لدينا حسب مسلمة لويس ديبرولي (1) :

p = h/λ

ولدينا العلاقة الخاصة بالموجات التي تجمع بين التردد والسرعة : λ = v/υ

نعوض في (1) :

p = h.υ/v

ثم نضرب الطرفين في السرعة v فنحصل على :

p.v = h.υ

وحدة كمية الحركة ضرب السرعة p.v هي الجول (j) ومنه نستنتج أن الطاقة الكلية للجسيم هي :

E = p.v = h.υ

إذن : E = h.υ

وهذه المعادلة هي نفسها التي قدمها كل من بلانك وأينشتاين لحساب طاقة الفوتون، لكن في حالتنا هذه فهي تمثل الطاقة الكلية للجسيمات المادية التي تسير بسرعة v غير نسبية أي صغيرة مقارنة مع سرعة الضوء، وللإشارة هنا فإن معادلة شرودينغر غير صالحة للجسيمات النسبية التي تسير بسرعة قريبة من سرعة الضوء كالفوتون مثلا.

نضرب الطرف العلوي في 2π ونقسم عليه :

E = h.υ.2π/2π = (h/2π).(2π.υ) = ℏω

لأن : ω = 2π.υ

ومنه :

E = ℏω (2)

وبهذا نحصل على المسلمة الشهيرة E =ℏω التي تعطي الطاقة الكلية للجسيمات والتي من خلالها تم الحصول على معادلة شرودينغر بالصورة أسفله !

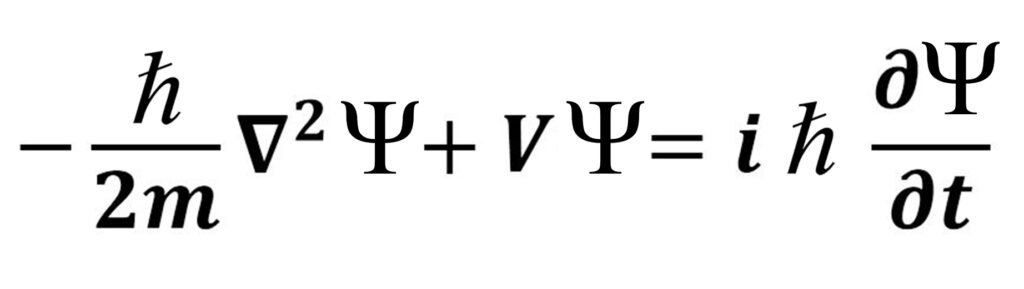
ونعلم حسب الميكانيك الكلاسيكية أن الطاقة الكلية للجسيمات تكتب كالتالي :

E = Ec + Ep

حيث الطاقة الحركية هي :

Ec = m.v²/2

وطاقة الجهد يرمز لها في ميكانيك الكم ب V عوض Ep :

Ep = V(r)

إذن :

E = m.v²/2 + V(r) (3)

ومنه حسب (2) و (3) فإن : ℏω = m.v²/2 + V(r)

نعلم أن : p = m.v

نضرب الطاقة الحركية في m ونقسم على m لكي نحصل على الطاقة الحركية بدلالة كمية الحركة p :

ℏω = (m².v²)/2m + V(r) = p²/2m + V(r)

وأخيراً نحصل على هذه المتساوية :

ℏω = p²/2m + V(r)

ومن خلال هذه المتساوية فقط يمكنك إستنتاج معادلة شرودينغر الشهيرة …

هل تريد البرهان على كيفية الحصول على معادلة شرودينغر؟

أترك لنا جوابك و رأيك في تعليق لكي نبرهن في المنشور القادم على معادلة شرودينغر من خلال هذه المتساوية الأخيرة التي حصلنا عليها.

إعداد : شعيب المستعين

مراجعة لغوية : نادية بوحفص

---

اقرأ الجزء الثاني :