كان العالم ماكس بلانك هو أول من طرح فكرة تكميم الضوء لحل مشكل الكارثة فوق البنفسجية ، وبذلك وضع علاقته الشهيرة كفرضية على أن الضوء لا يصدر عن الاجسام المشعة للموجات الكهرومغناطيسية بشكل متصل ، بل يخرج على شكل كمات منفصلة من الطاقة تحت ترددات مختلفة حسب العلاقة التالية :
E = n.h.f (1)
لكن هذا لا يعني أن الجسم مهما كانت حرارته سوف يشع طاقة كهرومغناطيسية تحت جميع الترددات الممكنة ، لكن هذه الترددات تكون مرتبطة بدرجة حرارة الجسم ، وهذا توضحه كذلك التجارب التي أجريت على الاجسام ، حيث تبين التجارب المبيانية للطاقة الصادرة عن الجسم بدلالة الترددات أن الطاقة تكون أغلبها مركزة حول تردد مركزي f₀ وحيد يتعلق بدرجة حرارة الجسم ، مع اشعاع طاقة اخرى اقل في باقي الترددات المحادية للتردد المركزي على اليمين وعلى اليسار كما يوضح الشكل في الصورة .
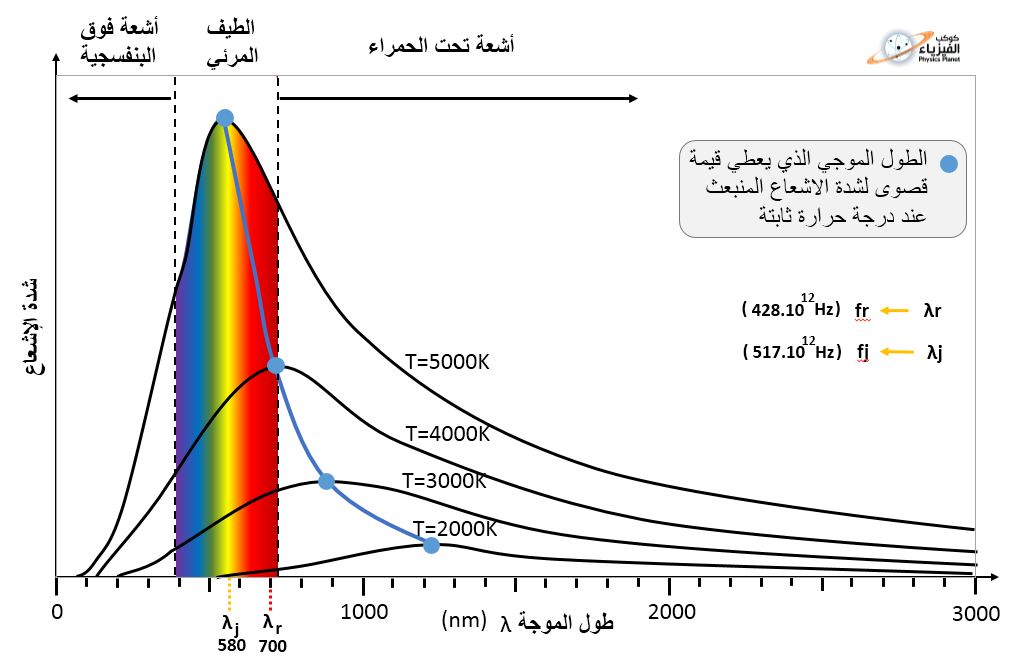
- نلاحظ من خلال النتائج التجربية على الشكل في الصورة أعلاه أنه بالنسبة لدرجة حرارة جسم عند T = 5000K ، فإن التردد المركزي f₀ الذي يبعث عنده الجسم الساخن أغلب طاقته الكهرومغناطيسية هو تردد اللون الاصفر الذي توجد عنده قمة المنحنى :
fj = 517.10¹² Hz
لكن لا يجب أن ننسى أن لهذا المنحنى وسع يشمل باقي الترددات على يمين و يسار التردد المركزي (اللون الأحمر) ، يعني أن الجسم يشع كذلك طاقة في باقي الالوان الاخرى لكن بدرجة أقل مقارنة مع اللون الأصفر .
- أما بالنسبة للجسم الذي يوجد عند درجة حرارة T = 4000K فإن قمة المنحنى تكون عند التردد المركزي للون الأحمر ، أي أن أغلب الطاقة الكهرومغناطيسية التي يبعث بها الجسم تتمركز حول الاشعة الحمراء حيث التردد :
fr = 517×10¹² Hz
و نفس الشيء يحدث هنا كذلك مقارنة مع المنحنى السابق ، فالجسم يشع طاقة كهرومغناطيسية في باقي ترددات الألوان الأخرى ، ويظهر من خلال المنحنى أن الجسم يشع كذلك طاقة في الاشعة تحت الحمراء .
استطاع ماكس بلانك أن يحل مشكلة الكارثة فوق البنفسجية بهذه الفرضية و التي اعطت نتائج تتوافق بشكل دقيق مع التجربة لكنه لم يكن يدري أنه بهذه الفرضية الجديدة خلق مشكل آخر يضرب الفيزياء الكلاسيكية في العمق ، وهو أن بهذه الطريقة جعل من الضوء و كأنه يخرج على شكل جسيمات او قذائف من الطاقة إن صح التعبير وليس كموجات متصلة كما كان سائد حسب الفيزياء الكلاسيكية و التي أدت الى بروز الكارثة فوق البنفسيجة الى الوجود .
ظل ماكس بلانك حائرا بين ما أقحمه في الفيزياء ، لأنه حل بذلك مشكل وأقحم الفيزياء في مشكل آخر حيث أنه حينها كان مؤكد بما لا يترك مجالا للشك أن الضوء موجات كهرومغناطيسية وليست جسيمات ، فيما بعد سوف تظهر مشكلة أخرى تسمى بظاهرة التأثير الكهروضوئي و التي تصدى لها أينشتاين لحلها ، لكنه تسلم علاقة ماكس بلانك لحل مشكلة التأثير الكهروضوئي وعندما حل المشكل وجد العلماء انفسهم أمام معضلة الخاصية الجسيمية للضوء ، وهو أن الضوء في الظاهرتين بدى و كأنه يتصرف كجسيم !
• اذا كان الضوء يتصرف كجسيم فلابد و أن يكون له كمية حركة p كباقي الجسيمات التي نعرفها ؟
لاحقاً سوف يتبين من خلال النسبية الخاصة لأينشتاين أن الجسيمات المتحركة بسرعة قريبة من سرعة الضوء يمكن حساب طاقتها بالعلاقة التالية :
E² = m².c⁴ + p².c²
لكن جسيم الضوء هذا لا يملك كتلة فهو عبارة فقط عن كمية من الطاقة تسير بسرعة الضوء :
اذن بما أن :
m = 0
فإن :
E² = p².c²
اذن طاقة جسيم الضوء هذا هي :
E = p.c (2)
من خلال (1) بالنسبة لجسيم ضوء واحد فإن n = 1 ومنه بمقارنتها مع (2) نحصل على :
p.c = h.f
وبما أن :
λ = c/f
فإن :
p.c = h.c/λ
وباختزال سرعة الضوء من كلا الطرفين نحصل على كمية الحركة للضوء الذي يسير بأقصى سرعة قصوى c :
p = h/λ
و هذا يمثل كمية الحركة لجسيم الضوء و قد اطلق فيما بعد عليه اسم الفوتون .
كانت هذه البداية نحو ميكانيك الكم وكان حينها الشغل الشاغل للعلماء هو تفسير اشعاع الضوء على المستوى الذري للعناصر الكيميائية ، وقد حاول العديد من العلماء دراسة الهيدروجين لأنه يشكل ابسط العناصر في الطبيعة ، لكونه يتكون فقط من الكترون و بروتون واحد ، بعد سلسلة من النماذج و التفسيرات التي كانت غالباً ما تظهر فيها مشاكل لعدم توافقها مع التجربة و الملاحظة ، خرج أخيرا نيلز بوهر بنموذج أبهر كل العلماء حينها لأنه استطاع من خلاله أن يفسر بدقة عالية كيفية اشعاع ذرة الهيدروجين للضوء و كيفية امتصاصه .
وكانت من بين الاضافات التي جعلت نموذج بوهر يستطيع تفسير ظاهرة اشعاع الهيدروجين ، هي مُسَلَّمته الشهيرة التي وضعها بدون برهان كما فعل ماكس بلانك في حالة اشعاع الضوء اذ العلاقة خرجت كفرضية من رأس ماكس بلانك :
قال نيلز بوهر لحل المشكل يجب أن نكمم العزم الحركي للالكترون حول النواة وبذلك وضع الفرض التالي :
L = n.h/2π
حيث h ثابت بلانك و n عدد صحيح اكبر من او يساوي 1 و L هو العزم الحركي للالكترون اثناء دورانه حول النواة و يكتب كالتالي :
L = p.r
حيث p كمية حركة الالكترون و r المسافة التي يبعد بها عن النواة .
بالنسبة للجسيمات فإن كمية الحركة هي كتلة الجسيم ضرب سرعته :
p = m.v
اذن مسلمة نيلز بوهر التي حلت المشكلة هي :
m.v.r = n.h/2π (3)
فيما بعد سوف تدور فكرة غريبة في رأس العالم لويس دي برولي ، إذ قال بما أن الضوء عبارة عن موجة ويتصرف كجسيم الا يمكن أن نقول بنفس المبدأ أن الجسيمات الصغيرة كالالكترونات و البروتونات يمكن ان تتصرف كموجات !
ووضع مسلمته الشهيرة حول طول موجة الجسيمات :
λ = h/m.v
• لكن كيف استطاع لويس دي برولي أن يحصل على هذه العلاقة التي تربط كمية حركة الجسيم بطول موجته ؟
حسناً نعلم أولا أن الالكترون جسيم له كتلة وسرعة و بما أن حركة الالكترون كجسيم حول النواة دائرية فإن العلاقة التي تربط بين سرعة انتقاله حول النواة و سرعته الزاوية هي :
v = r.ω (4)
وبما أننا نفترض أنه يمكنه أن يتصرف كموجة فإنه يمكن أن نستغل علاقة التبدد التي تربط بين سرعة انتقاله و تردده الزاوي :
ω’ = k.v
حيث k هو العدد الموجي :
k = 2π/λ
بما أن الالكترون الآن يفترض أنه موجة وجسيم في نفس الوقت فإن تردده الزاوي هو نفسه سرعته الزاوية و منه :
ω’ = ω
إذن :
v = ω/k (5)
: وبمقارنة (4) و (5) نحصل على
r.ω = ω/k
إذن :
r = 1/k = λ/2π
ومنه نحصل على العلاقة بين محيط المسار الدائري الذي يدور فيها الالكترون حول النواة وبين طول موجته :
2π.r = λ
هنا انبهر لويس دي برولي ولم يستطع ان يستوعب أنه قد فعلها ، المسار الذي يقطعه الالكترون حول النواة قد يكون في علاقة تناسبية مع طول موجته ، وهنا بما أن الالكترون قد لا يتواجد فقط في مسار واحد حول النواة لأنه قد يصعد الى مدار أعلى كما قد يهبط الى مدار أدنى كما يقول بذلك نموذج نيلز بوهر ، فإن هذا المسار يجب أن يكون متناسب طرديا مع عدد اطوال الموجات في كل المسارات الممكنة ومنه وضع لويس دي برولي العلاقة التالية :
2π.r = n.λ (6)
حيث n عدد صحيح طبيعي اكبر من او يساوي 1 مثلا اذا اخترنا شعاعات لمسارات مختلفة فإنه يمكننا كتابة التالي :
2π.r₁ = λ
2π.r₂ = 2λ
2π.r₃ = 3λ
وهذه العلاقة كانت هي مفتاح اللغز حيث أن لويس دي برولي افترض ان الالكترونات تدور في مسارات متموجة حول النواة على شكل موجات متوقفة ، ولكي يكون هذا الالكترون مستقر في مساره يجب أن يكون عدد الموجات يساوي عدد طبيعي وليس عدد كسري به فاصلة و لهذا لا يمكنه ان يتواجد الا بالمسارات التي لها عدد اطوال موجات مكتمل كالتالي :
λ , 2λ , 3λ , 4λ , 5λ …
ولا يمكن أن تجد مثلا مسار بهذه القيم :
λ/2 , 5λ/3 , 7λ/5 , 4λ/3 , 11λ/2
لأنها تعتبر مسارات غير مستقرة أنظر الصورة :

أراد دي برولي أن يفسر حركة الالكترون حول النواة بالموجات المتوقفة (أنظر الصورة a باللون الأحمر) ، هذا النوع من الموجات لا ينتشر في الاوساط كما تفعل ذلك الموجات المنتقلة (أنظر الصورة b) . وإنما يظل في حالة اهتزازية توافقية في نفس المكان كأوتار الكيتار مثلا ، حيث تكون هناك عقد ثابتة في الموجة لا تتحرك و هناك بُطُون تتحرك الى أعلى ثم الى أسفل في نفس المكان .
هذا الوصف جعل من الالكترون عبارة عن موجة موتقفة توجد في كل الأماكن حول النواة وليس فقط في مكان محدد كما تقول بذلك النظرية الجسيمية للإلكترون ، الأمر كان معقد جداً وصعب الفهم لأننا لا نستطيع أن نتخيل أن الالكترون يمكن أن يكون فعلا عبارة عن موجة حقيقية ، و الاغرب في الأمر هو مالذي يتموج اذا كان الالكترون جسيم ، كانت هناك العديد من الفرضيات وكأن الموجة تحمل الالكترون أو أنها عبارة عن ذيل له لكن كل هذه التفسيرات باءت بالفشل في الأخير .

وانطلاقا مما توصل إليه لويس دي برولي ومن مسلمة نيلز بوهر سوف يستطيع أن يبرهن على العلاقة التي يمكن من خلالها حساب طولة موجة الجسيم .
: من خلال علاقة نيلز بوهر (3) لدينا
m.v.r = n.h/2π
اذن :
m.v.2π.r = n.h (7)
: لدينا من خلال ما توصل اليه لويس دي برولي (6)
2π.r = n.λ
: نعوض في (7)
m.v.n.λ = n.h
نختزل ب n من كلا الطرفين فنحصل على العلاقة الشهيرة التي وضعها لويس دي برولي لحساب طولة موجة الجسيمات :
λ = h/m.v
▪ خلاصة
استطاع لويس دي برولي بحدسه الثاقب ان يتنبأ بإمكانية تصرف الجسيمات كموجات ، و استطاع بهذه الطريقة الرياضية الجميلة أن يستخرج طول موجة الجسيمات ، وبعد اجراء التجارب تبين أن العلاقة التي وضعها دي برولي تتوافق تماماً مع النتائج التجربية مما أكد صحة نموذجه الرياضي . استطاع كل من العالمين دي برولي و نيلز بوهر أن ينالا جائزة نوبل على اعمالهما ومساهماتهما العظيمة في تقدم الفيزياء .
لكن سوف يتبين فيما بعد قُصر نموذج نيلز بوهر على تفسير طيف الانبعاث و الامتصاص عند باقي العناصر الثقيلة ، وكذلك التفسيرات الفيزيائية التي قدمها دير برولي بخصوص تحرك الالكترون على شكل موجات متوقفة حول النواة . لكن فيما يخص تصرف الجسيمات كموجات ظلت حقيقة علمية و كذلك علاقته التي تعطي الطول الموجي للجسيمات . كانت هذه فقط البداية نحو بحر ميكانيك الكم الذي سوف يستمر الغوص فيه فيما بعد لصبر اغوار المادة واكتشاف غرائبها وعجائبها الفريدة .
▪مصطلحات
Catastrophe UV : الكارثة فوق البنفسجية
Fréquence centrale : تردد مركزي
Effet photoélectrique : التأثير الكهروضوئي
Moment cinétique : العزم الحركي
Quantité de mouvement : كمية الحركة
Postulat : مُسَلَّمة
Noyau : نواة
Dispersion : تبدد
Pulsation : fréquence angulaire : النبض : التردد الزاوي
Nombre d’onde : العدد الموجي
Longueur d’onde : الطول الموجي
Onde stationnaire : موجة مستقرة أو متوقفة
Onde progressive : موجة منتقلة أو متقدمة
Ventre : بطن
Nœud : عقدة
تحرير : شعيب المستعين
المراجعة العلمية :
حسام بنكروم
اسماعيل بنشيخ
التدقيق اللغوي : نادية بوحفص
تصميم الصور الثايتة : رشيد هروس
تصميم الصور المتحركة : عمر عسناوى






2 Comments
Merci c’est intéressant j’ai juste une petite question concernant la relation entre la
fréquence centrale et la température dans la catastrophe UV .vous n’avez pas mentionné la relation de plank qui donne la densité de puissance monochromatique puis après à l’aide d’une intégration on remonte à la loi de Stéphane est ce que vous pouvez donner plus de détails
شكرا سي حمزة على الاشارة … ما جاء في مقدمة المقال هو فقط تقديم صغير لأن المقال لم يكن غرضه التوسع في ما يخص الكارثة فوق البنفسجية وانما يريد البرهنة على مسلمة دي برولي ، لكن سوف نتطرق لما أشرت اليه في مقال مفصل يكون اكثر دقة ان شاء الله .
مرحبا مرة اخرى وشكرا على تعليقك ?