الأنتروبي S هي ” دالة حالة ” أي انها لا تتعلق بالمسار المُتبع ولكن فقط بالحالة البدئية و النهائية للنظام ، الأمر شبيه بطاقة الوضع الثقالية Ep الناتجة عن الجاذبية فهي كذلك دالة حالة لأنها لا تتعلق الا بالحالة البدئية و الحالة النهائية للنظام .
ΔEp = Epf – Epi
تخيل أنك واقف على سطح الأرض و يوجد جسم في يدك على مسافة h من سطح الأرض ، فسواء أسقطت الجسم مباشرة عمودياً على سطح الأرض أو قذفته في الهواء ثم سقط بعد ذلك على سطح الأرض ، فطاقة الوضع الثقالية عند سطح الأرض سوف تكون هي نفسها في كلا الحالتين لأن طاقة الوضع لا تتعلق بالمسار المتبع وانما فقط بنقطة البداية ونقطة النهاية ، الصورة (1) .
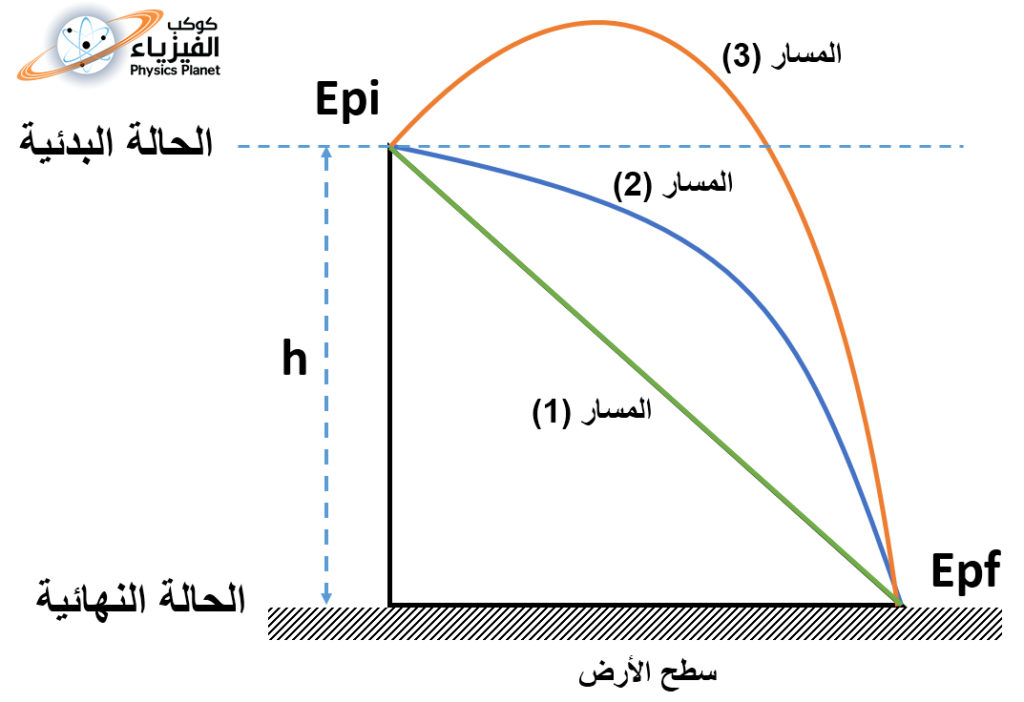
ولهذا فالتغير طاقة الوضع الثقالية بين الحالة البدئية و الحالة النهائية يكتب كالتالي :
ΔEp = Epf – Epi = m.g.h
حيث h هي المسافة الفاصلة بين الموضع الذي كان يتواجد به الجسم في الحالة البدئية و الموضع الذي أصبح يوجد فيه في الحالة النهائية ، أي هو الإسقاط العمودي نحو سطح الأرض بين الموضعين .
فكذلك دالة الأنتروبي فهي لا تتعلق إلا بالحالة البدئية و الحالة النهائية للنظام وتكتب كالتالي :
ΔS = Sf – Si
أولا يجب أن نختار النظام الذي سوف نشتغل عليه مع وضع بعض الفرضيات و التقريبات التبسيطية حتى يسهل علينا دراسة وتحليل وفهم الموضوع جيداً .
▪الحالة الأولى
سوف نختار النظام هنا عبارة عن غاز كامل أحادي الذرة ، أي أنه لا يتكون الا من ذرات وليس فيه جزيئات ، و درجة حرارته هي T ، و يوجد هذا الغاز داخل نصف أسطوانة مقسومة بحاجز لا يسمح بمرور الحرارة الى النصف الآخر الذي لا يوجد فيه إلا الفراغ ، نعتبر أن هذه الأسطوانة معزولة حرارياً أي أنها لا تسمح بدخول أو خروج الحرارة في كل جوانبها إلا من مكان صغير من أسفلها سوف نستغله لتسخين الغاز ، الصورة (2) ، ولكي أوضح الأمر جيداً من وجهة نظر ميكروسكوبية فإن الجزيئات و الذرات التي تكون جدار الأسطوانة سوف تكون في سكون مطلق و لا تستطيع الحركة إذا ما صدمتها ذرات الغاز التي توجد بداخلها أو بخارجها ، و بمعنى آخر أنه ليس هناك أي تبادل طاقي بين مكونات الوسط الداخلي و الخارجي لجدار الأسطوانة ، مثلا إذا كانت ذرة لها طاقة حركية معينة وصدمت الجدار سوف يتغير اتجاهها دون ان تفقد أي شيء من طاقتها الحركية بسبب الاصطدام مع جدار الأسطوانة .
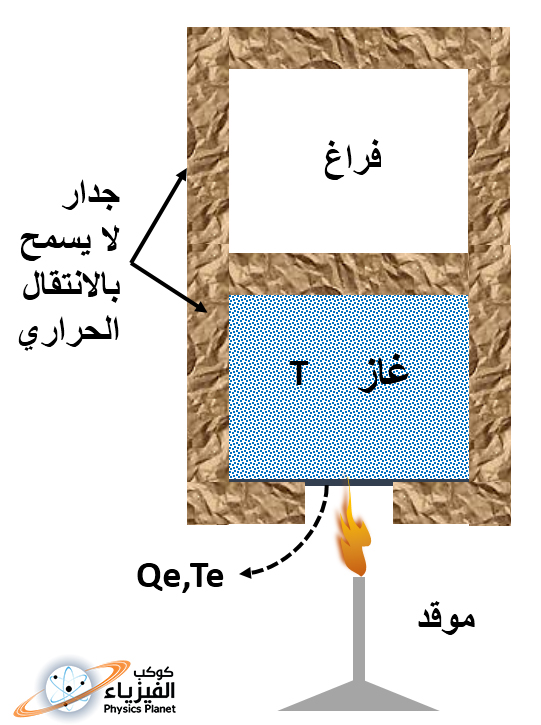
سوف نقوم حالياً بوضع جهاز تسخين من ذلك المكان الذي يوجد أسفل الأسطوانة مما يعني أننا سوف نمُد الغاز بداخل الأسطوانة بالطاقة الحرارية الشيء الذي سوف ينتج عنه إرتجاج أكبر وفوضى وعشوائية في تنقل ذرات الغاز وهذا هو ما يسمى بازدياد الأنتروبي أي إزدياد الفوضى .
دعنا نلقي نظرة عن كثب من وجهة نظر ميكرسوكبية لنعلم ما الذي يحدث بالضبط !
الحرارة ليست في الأصل الا طاقة حركية للجزيئات و الذرات ، و تسخين غاز يعني رفع طاقته الحركية ، إذن كيف يتم الأمر ؟
اللهب الذي نسخن به اسفل الأسطوانة هو مجرد طاقة ناتجة عن تفاعل كيميائي يسمى بالإحتراق ، هذه الطاقة تُكسب جزيئات الجدار في أسفل الأسطوانة طاقة حركية كبيرة مما يجعلها تبدأ بالإرتجاج و الإهتزاز بعنف ، ارتجاج جزيئات الجدار بعنف يُنقل الى ذرات الغاز الملامسة للجدار من الداخل فتبدأ ذرات الغاز القريبة من الجدار هي الأخرى بالإرتجاج و الاهتزاز بعنف ، فتبتعد بفعل اكتسابها سرعات كبيرة وتأتي ذرات أخرى مكانها فتكتسب هي الأخرى طاقة حركية كبيرة وتبتعد ويستمر هذا الإنتقال الطاقي بين جزيئات الجدار و ذرات الغاز حتى تصبح الذرات التي تكون الغاز ذات طاقة حركية كبيرة ، وبسبب هذه الطاقة الحركية التي اكتسبتها ذرات الغاز سوف تعُم الفوضى و الحركة العشوائية داخل الأسطوانة وهذا هو الإزدياد في الأنتروبي لأن الأنتروبي هو قياس للإزدياد في الفوضى و الحركات العشوائية ، إذن العشوائية تزداد بفعل اكتساب الطاقة الحرارية .
فحسب القانون الثاني لنيوتن يمكن أن نقول أن جزيئات الجدار تعتبر كقوى خارجية تطبق قوة على النظام الداخلي أي ذرات الغاز ، فكل ذرة غاز تقترب من جزيئة الجدار تكسبها زخم حركي بفعل الاصطدام معها أي تجعلها تتسارع لتزيد من سرعتها إذن إزدياد في الطاقة الحركية .
يسمى هذا الأنتروبي الناتج عن التبادل الحراري بالانتروبي المتبادل ونرمز له ب : Se
إذن التغير في الانتروبي بين الحالة البدئية والحالة النهائية يكتب كالتالي :
ΔS = Sf – Si = Se
إذن الأنتروبي النهائي للنظام هو :
Sf = Si + Se
لا ننسى أن العملية العكسية سوف تجعل أنتروبي النظام يتناقص أي عوض أن تزود النظام بالطاقة الحرارة نسلب منه الطاقة الحرارية فهذا سوف يجعل الأنتروبي النهائي أقل من الأنتروبي البدئي وهذا ما تفعله الثلاجة فهي تسلب من الأشياء الموضوعة داخلها الطاقة الحرارية مما يجعل أنتروبي النظام النهائي يتناقص .
يتم تحديد الانتروبي المتبادل بالعلاقة التالية :
Se = Qe/Te
حيث Qe هي الطاقة الحرارية المتبادلة و Te هي درجة حرارة الوسط الذي يزود النظام بالطاقة الحرارية أو يأخذها منه وهنا Te تمثل الجزء السفلي للأسطوانة الذي تدخل عبره الطاقة الحرارية للنظام ، لكن يجب أن نلاحظ أن الطاقة الحرارية المتبادلة Qe يمكنها أن تكون موجبة أو سالبة حسب الإتفاق فإذا كان الجسم يؤخذ حرارة من الوسط الخارجي فهي موجبة وإذا كان هو من يعطي طاقة حرارية للوسط الخارجي تكون سالبة ولهذا فالأنتروبي المتبادل Se يمكن أن يكون سالباً أو موجباَ . فإذا كان موجب يزداد انتروبي النظام واذا كان سالباً يتناقص أنتروبي النظام .
▪الحالة الثانية
الآن سوف ننتقل إلى إزدياد في الأنتروبي دون تبادل حراري بين النظام مع باقي العالم الخارجي :
نأخذ نفس الأسطوانة السابقة المعزولة حرارياً و التي يملأ الغاز الكامل الأحادي الذرة نصفها و النصف الأخر به فراغ يفصل بينهما جدار عازل للحرارة ، الآن سوف نقوم بعزل حراري حتى للمنطقة السفلى للأسطوانة والتي كنا نزود منها النظام بالطاقة الحرارية ، إذن نظامنا حالياً أصبح معزول بصفة مطلقة مع الخارج ، الصورة (3) .
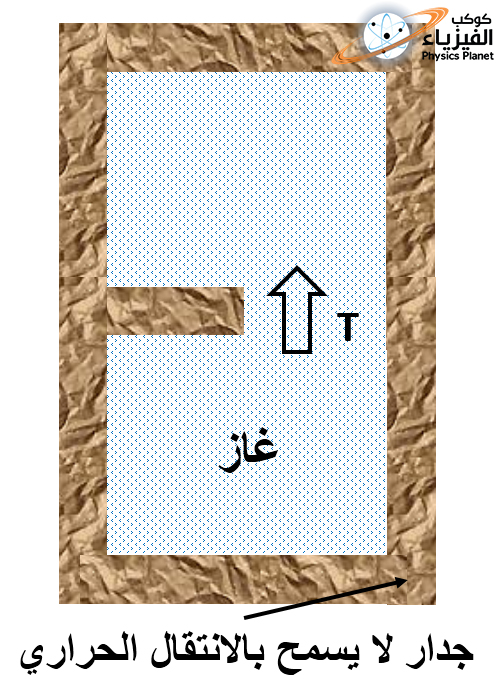
سوف نقوم الآن بسحب ذلك الجدار الذي يقسم الأسطوانة الى نصفين مما سوف يجعل الغاز يملأ كل الأسطوانة تلقائياً ودون تدخل خارجي أو تزويد بالطاقة !
هنا نقول أن الفوضى هي خاصية من خاصيات الطبيعة و أن كل شيء يميل الى الفوضى و الحركة العشوائية تلقائياً وأن هذا قانون طبيعي ! هذا ليس صحيح وناتج فقط عن عدم قدرتنا على دراسة النظام ميكانيكياً على المستوى الميكروسكوبي .
فقط عبر مبدأ القصور أو ما يسمى بالقانون الأول لنيوتن وكذلك قانون إنحفاظ كمية الحركة يمكننا تفسير حدوث هذا الأمر تلقائياً دون حاجة الى الطاقة او تدخل خارجي ، فما يحدث هو أننا قبل أن نزيل الجدار الغاز كانت لديه حرارة معينة أي أن الذرات لها طاقات حركية أو بمعنى أدق أن لكل ذرة كمية حركة p تكتب كالتالي :
p = m.v
فحسب القانون الأول لنيوتن فأي جسم له سرعة معينة سوف يستمر في الحركة طالما ليست هناك قوة توقفه او تزيد من سرعته ، وبما أننا إفترضنا جزيئات الجدار لا تتبادل الطاقة مع الغاز فأي تصادم بينهم لن يجعل الطاقة الحركية لذرات الغاز تتناقص ولهذا فهناك انحفاظ في الطاقة الحركية أي انحفاظ في كمية الحركة p ولهذا فذرات الغاز يمكنها أن تستمر في السير دون توقف مهما كان الحجم الذي توجد فيه ، ولهذا فكلما ازداد الحجم الذي يوجد فيه الغاز فإن الغاز سوف يتحرك فيه بالكامل بكل حرية ودون احتياج الى طاقة .
وهذا الانتشار في الحجم الكامل هو ما نطلق عليه ازدياد الفوضى تلقائياً لكن فهو حسب مبدأ القصور الذاتي وانحفاظ كمية الحركة فهذا ما يجب أن يقع تلقائياً وليس هناك ميول الى الفوضى ، فالفوضى التي نتكلم عليها هي أننا لن نستطيع أن ندرس ميكانيكياً كل على حدى ملايير الذرات بقوانين نيوتن لأن الأمر مستحيل .
هنا نلاحظ أن ازدياد الفوضى ليس ناتج عن تبادل الطاقة الحرارية وانما فقط بسبب القصور الذاتي للذرات إذن يجب وضع متغير آخر يسمى بالانتروبي المُخلق من طرف النظام ويرمز له ب : Scrée
إذن التغير في الأنتروبي بين الحالة البدئية و الحالة النهائية يكتب كالتالي :
ΔS = Sf – Si = Scrée
إذن الأنتروبي النهائي للنظام يكتب كالتالي :
Sf = Si + Scrée
هنا الانتروبي المُخلق لا يمكن أن يكون سالباً فهو إما موجباً أو منعدماً لأن الجزيئات لا يمكن أن تترك مساحة فارغة في الحجم الذي تتواجد به و تتكتل لوحدها في حجم آخر أقل فهي كلما إعطيتها مساحة أكبر توسعت فيها وشغلتها كلها ولهذا فالانتروبي المُخلق دائما أكبر من أو يساوي صفر .
Scrée ≧ 0
▪الحالة العامة
خلال هذا التحليل قمنا بدراسة الحالتين بانفصال لنسهل الدراسة فقط لكن في الحالة العامة نكتب :
ΔS = Sf – Si = Se + Scrée
Sf = Si + Se + Scrée
وعلى حساب المعطيات الوضعية يمكن حساب الأنتروبي النهائي .
تغير الأنتروبي ΔS بصفة عامة دائما أكبر من أو يساوي صفر ولا يكون أبداً أصغر من الصفر في التحولات التلقائية في الطبيعة :
ΔS ≧ 0
ومنه فإن :
Sf = Si + Se + Scrée ≧ Si
لا يمكن أبداً أن يكون تحولاً تقائياً في الطبيعة بحيث نجد أن الأنتروبي النهائي أصغر من الأنتروبي البدئي .
أي أن هذه الحالة :
Sf ≦ Si
مستحيلة تلقائياً في الطبيعة !
▪ملاحظة
كما لا ننسى أننا أخذنا الحالة المثالية للغاز وهو غير موجود في الطبيعة وكذلك أخذنا الحالة المثالية للأسطوانة التي لا تسمح بالانتقال الحراري وهي غير موجودة في الطبيعة … ومنه فيجب الأخذ بعين الاعتبار خلال الحسابات كل هذه التقريبات و الفرضيات التي قمنا بها ، لكن المتخصصين في المجال لديهم طرق اخرى للحساب لأن الغرض من هذا المنشور كان فقط استيعاب مفهوم الأنتروبي وليس شرح طرق حسابه .
الطريقة التي أخذنا هنا في عدم تبادل الحرارة بين الاسطوانة و الوسط الخارجي هي مثالية ولا توجد في الواقع لكن هناك ألية أخرى تسمى بمنظم الحرارة (ترموستات) بالترموسا و التي تعزل حراريا ما يوجد بداخلها على الوسط الخارجي سوف أتكلم عن انواع الانتقال الحراري و آلية عمل هذا الجهاز في منشور آخر .
▪حالة خاصة “التحول الحلقي “
التحول الحلقي ومعناه أن النظام ينطلق من الحالة البدئية ويقوم بسلسلة من التحولات ثم يعود الى الحالة البدئية وبالتالي سوف تكون الحالة النهائية لهذه السلسة من التحولات هي الحالة البدئية نفسها :
نفترض مثلا أن تحول النظام ينطلق من الحالة البدئية A ثم يصل الى B وبعدها الى C ثم الى D ثم من D يعود الى A .
لدينا إذن الحالة البدئية Si هي SA و الحالة النهائية Sf هي SA وبما أن الأنتروبي “دالة حالة” اي لا تتعلق الا بالحالة البدئية و الحالة النهائية للنظام فإنه يمكن كتابة التالي :
ΔS = Sf – Si = SA – SA = 0
إذن :
Se + Scrée = 0
ومنه :
Se = – Scrée
نعلم حسب ما سبق أن الأنتروبي المُخلق دائما أكبر من أو يساوي صفر :
Scrée ≧ 0
ومنه فإن الأنتروبي التبادلي أصغر من أو يساوي صفر :
Se ≦ 0
فإذا كان الأنتروبي المُخلق Scrée منعدم خلال هذا التحول الحلقي معناه أن الأنتروبي التبادلي Se يجب أن يكون بالضرورة منعدم وهذا يعني أنه خلال هذه السلسلة المغلقة من التحولات ، النظام لم يتبادل أي طاقة حرارية كلية مع الوسط الخارجي .
أما إذا كان الأنتروبي المُخلق غير منعدم فإنه سوف يكون بالضرورة ذا قيمة موجبة وبالتي فإن الأنتروبي التبادلي يجب أن يكون سالباً ومنه فإن النظام خلال هذا التحول الحلقي أعطى طاقة حرارية للوسط الخارجي .
▪خلاصة
كخلاصة الأنتروبي هو قياس لفوضى النظام الناتجة عن التبادل الحراري بين النظام و الوسط الخارجي والذي ينتج عنه أنتروبي تبادلي Se و كذلك عن إنحفاظ كمية الحركة لمكونات النظام والذي ينتج عنه أنتروبي مُخلق Scrée .
▪طريقة أخرى لحساب الأنتروبي
هناك طريقة أخرى لبولتزمان تعتمد على الفيزياء الإحصائية لحساب الأنتروبي حسب العلاقة الثالية :
S = Kb.Log(Ω)
حيث Kb ثابت بولتزمان و Ω تسمى عدد المكونات النظام .
لكن لن نتكلم عنها في هذا المقال لأنها تعتمد على الإحتمالات .
▪مصطلحات :
Fonction d’état : دالة الحالة
Entropie : أنتروبي
Entropie échangé : الانتروبي المتبادل
Entropie crée :الانتروبي المُخلق
Variation de l’entropie : تغير الأنتروبي
Désordre : فوضى
Gaz parfait : غاز كامل
Calorifigé : معزول حرارياً
Thermostat : منظم الحرارة
Transformation cyclique : التحول الحلقي
تحرير : شعيب المستعين







One Comment
جزاك الله خير رغم أنني سبق وأن درست الديناميكا الحراية هذه أو مرة أفهم فيها فعلا دآلة الإنتروبي ودلالتها الفيزيائية أتساءل لماذا الدكاترة لا يركزون فقط على تلقيننا طرق تطبيق القوانين الفيزيائية دون فهمها ؟ على أي بوركت أخي شعيب ❤✌